5. AVD matemaatilised alused

Navier–Stokesi võrrand

Navier–Stokesi võrrand on arvutusliku voolise dünaamika keskne matemaatiline mudel. See kirjeldab voolise liikumist, ühendades massi, impulsi ja energia jäävuse seadused ühtseks osatuletistega diferentsiaalvõrrandite süsteemiks. Võrrand on mittelineaarne ja seotud, mis tähendab, et tundmatud (rõhk, kiirus ja temperatuur) mõjutavad üksteist samaaegselt. Üldkujul on impulsi jäävuse võrrand esitatud kujul:

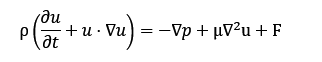
Siin tähistab ρ voolise tihedust, u kiirusvektorit, p rõhku, μ dünaamilist viskoossust ja F välisjõud. Võrrandi vasakul poolel on inertsi ja konvektsiooni liikmed, paremal poolel rõhu gradient, viskoossusjõud ja välised mõjud.

Navier–Stokesi võrrandit ei ole võimalik enamikul juhtudel analüütiliselt lahendada, sest see sisaldab mittelineaarseid ja seotud osatuletisi. Lahendamiseks kasutatakse arvutuslikke meetodeid, mis põhinevad diskretiseerimisel. Diskretiseerimine tähendab, et pidev arvutusruum jaotatakse väikesteks osadeks, mille kohta arvutatakse ligikaudne lahendus.

 Lõplike mahuelementide meetod

FloEFD tarkvara rakendab lõpliku mahuelemendi meetodit, mis on üks levinumaid diskretiseerimistehnikaid. Selle meetodi puhul jaotatakse arvutusruum kontrollmahtudeks, mida nimetatakse lahtriteks või võrgusilmadeks. Iga kontrollmahu kohta esitatakse valitsevad võrrandid integraalkujul, mis tagab jäävuse seaduste täitmise lokaalselt. Näiteks üldine integraalkujuline vorm on:

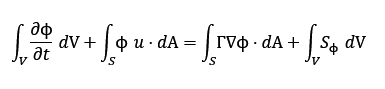
kus
ϕ – üldine suurus (rõhk, temperatuur, kiiruskomponent),
V – kontrollmaht,
S – pind,
Γ – difusioonikoefitsient,
Sϕ – allikaterm.

Siin on ϕ üldine suurus, mis võib tähistada rõhku, temperatuuri või kiiruskomponenti, V kontrollmaht ja S selle pind. Vasakul poolel on ajamuutus ja konvektsioon, paremal poolel difusioon ja allikaterm. FloEFD-s paiknevad kontrollmahud geomeetria sees ja piirpindade lähedal. Üldiselt kasutatakse paralleelseid risttahukaid. Piirpindade lähedal, kus voolise ja tahke keha kontakt on oluline, kasutatakse keerukama kujuga hulktahukaid (polüeedreid). Põhimuutujad viidatakse kontrollmahu massikeskmetele, mis lihtsustab arvutust ja tagab täpsuse.

Lõpliku mahu meetodi eelis on see, et see säilitab füüsikaliste suuruste jäävuse igas kontrollmahus, mis on kriitiline insenerisimulatsioonide usaldusväärsuse jaoks. FloEFD integreerib selle meetodi CAD-keskkonda, võimaldades inseneridel luua võrgustiku automaatselt ja määrata piiritingimused otse geomeetriale.