1. Solid Edge FloEFD ja arvutuslik voolu dünaamika
| Õpikeskkond: | Eesti Maaülikooli Moodle |
| Kursus: | Simulatsioonid |
| Raamat: | 1. Solid Edge FloEFD ja arvutuslik voolu dünaamika |
| Printija: | Külaliskasutaja |
| Kuupäev: | esmaspäev, 26. jaanuar 2026, 02.18 AM |
Kirjeldus
Ülevaade FloEFD tarkvarapaketist ja arvutusliku voolise dünaamika põhimõtetest
1. Sissejuhatus
AVD – Arvutuslik voolise dünaamika
AVD (Computational Fluid Dynamics, CFD) on meetod, mille abil simuleeritakse vooliste (vedelike, gaaside ja nende segude) liikumist ning koostoimet pindade ja struktuuridega. Eesti keeles on kasutusel mitmeid tõlkevariante: arvutuslik voolise dünaamika, arvutuslik voolu dünaamika, arvutuslik vedelike dünaamika. Käesolevas materjalis kasutatakse lühendit AVD, mis on autori loodud suupärasem termin. Samuti leiab autor, et parim tõlge inglisekeelsele terminile fluid on voolis, sest see kätkeb endas kõikvõimalikke voolavaid aineid, mitte ainult vedelikke. Materjalis on kasutatud mõnel juhul ingliskeelseid termineid vaid seetõttu, et kasutatav tarkvara on inglisekeelne ja õppuritel on seeläbi parem arusaam, milliseid töökäske tarkvaras kasutada.
AVD eesmärk on lahendada voolamise käitumist kirjeldavad Navier–Stokesi võrrandid, tuginedes matemaatilistele mudelitele ja numbrilistele meetoditele. Meetod võimaldab analüüsida keerukaid nähtusi, nagu turbulents, soojusülekanne ja mitmefaasilised voolud, mida on füüsilises katses keeruline või kulukas uurida.
FloEFD arvutusprotsessis jaotatakse arvutusruum kontrollmahtudeks, mida nimetatakse lahtriteks või võrgusilmadeks (ingl. cells). AVD tugineb lõpliku mahu meetodile (Finite Volume Method, FVM), kus valitsevad võrrandid (massi, impulsi ja energia jäävuse seadused) lahendatakse integraalkujul iga kontrollmahu kohta. Erilist tähelepanu pööratakse piirpindadele, kus voolis puutub kokku tahke kehaga, sest seal määravad voolukiiruse, rõhu jaotused ja süsteemi dünaamika.
AVD on inseneritöö lahutamatu osa, kuna see võimaldab optimeerida konstruktsioone, vähendada energiakulu ja hinnata töökindlust enne füüsilise prototüübi loomist. FloEFD tarkvara Solid Edge keskkonnas rakendab neid meetodeid otse CAD-projekteerimise kontekstis, muutes simulatsioonid inseneridele kättesaadavaks ja praktiliseks.
2. Mõisted
Arvutusdomeen- arvutuspiirkond, kus toimuvad voolu- ja soojuslevi arvutused. Kõik, mis jääb selle kasti sisse, kuulub analüüsi alla.
Arvutusvõrk (arvutusvõrgustik)- koosneb lahtritest (võrgusilmadest), mis võivad olla voolises või selle piiril. Voolise ja tahke keha piiril asuvad lahtrid määravad arvutuste täpsuse.
Isoline ehk isokõver(joon)- kahemõõtmeline joon (nt lõikepinnal), millel parameeter on konstantne. Näiteks rõhu isokõver näitab lõikepinnal kõiki punkte, kus rõhk on sama.
Isosurface ehk isopind- kolmemõõtmeline pind, millel mingi parameeter (nt temperatuur, rõhk, kiirus) on konstantne kogu pinna ulatuses. Näiteks temperatuuriga 50 °C isopind näitab ruumis kõiki punkte, kus temperatuur on täpselt 50 °C.
Iteratsioon- üks arvutuse samm, mille käigus FloEFD lahendab voolise ja soojuslevi võrrandeid arvutuspiirkonnas, uuendab lahtrite väärtusi ja kontrollib koonduvust. Matemaatiline üldkuju:
Kanal- FloEFd kontekstis kasutatakse mõistet kitsas kanal voolukanalite kirjeldamiseks, kus kahe vastastikku asetseva pinna vahemaa on kogu arvutuspiirkonna suhtes väike.
Kartesiaanvõrk- koordinaatsüsteemi järgi joondatud regulaarvõrk, kus võrgu lahtrid on kõik samas suunas ja suuruses.
Kontrollmahu piirid- vastavad füüsilistele piiridele, kus mõjuvad pinnajõud (rõhujõud, hõõrdejõud) ja massijõud.
Koonduvus- arvutusprotsess on jõudnud stabiilsesse olekusse, kus lahenduse muutused iteratsioonide vahel on väga väikesed. FloEFD kontrollib koonduvust, jälgides mis hetkel valitud eesmärkide väärtused enam märkimisväärselt ei muutu.
Lõpliku suurusega mahuelementide (kontrollmahtude) meetod LMM (Finite Volume Method, FVM)- Lõpliku suurusega mahuelementide meetod on arvutuslik tehnika, mida kasutatakse osatuletistega diferentsiaalvõrrandite lahendamiseks voolamise ja soojuslevi simulatsioonides. Selle meetodi põhimõte on jaotada arvutuspiirkond väikesteks osadeks, mida nimetatakse kontrollmahtudeks (või lahtriteks, võrgusilmadeks). Iga kontrollmahu kohta rakendatakse füüsikalised jäävuse seadused – massi, impulsi ja energia jäävus – integraalkujul.
Piirilahtrid (boundary cells)- need asuvad voolise-tahke keha kontaktaladel (nt toru sein, pais, lüüs). Neile rakendatakse piiritingimusi (kiirus, rõhk, temperatuur).
Pinna eesmärkide tabeli selgitus:
Average ehk keskmine väärtus arvutatakse valitud pinna kohta, võttes arvesse ainult pinna pindala. See tähendab, et iga lahtri panus keskmisesse sõltub sellest, kui suure osa pinnast ta katab, sõltumata voolamise intensiivsusest. Näiteks kui sisselaske ava lähedal on külmem voolis ja ava keskel kuumem, siis keskmine temperatuur arvutatakse pindala kaalutud keskmisena, mistõttu külmad piirkonnad seina lähedal mõjutavad tulemust sama palju kui kuum vool keskosas. Selline lähenemine sobib olukordadesse, kus huvipakkuv on geomeetriline pind ja selle parameeter, mitte voolamise dünaamika.
Bulk Average ehk massvoolu keskmine arvestab lisaks pindala kaalule ka vooluhulka läbi pinna, st massvoolu. See tähendab, et piirkonnad, kus vooluhulk on suurem, mõjutavad keskmist rohkem. Näiteks toru ava puhul, kus voolu tuum on kuum ja liigub suure kiirusega, annab see piirkond bulk average arvutuses suurema kaalu kui külmad ja aeglased kihid seina lähedal. Seetõttu vastab bulk average paremini tegelikule olukorrale, kus voolamise mõju määrab mitte ainult pindala, vaid ka voolamise intensiivsus ja massvool.
3. Tootjapoolne abi
· Programmisisene abi, mis avaneb brauseris raamatuna
o 
· Solid Edge support Center
o https://docs.sw.siemens.com/en-US/doc/246738425/PL20230918048379379.xid1854090/xid706512
· FloEFD lühike abiinfo
o https://docs.sw.siemens.com/en-US/doc/246738425/PL20230918048379379.validate/xid1554957
· Siemens Xcelerator Academy tasuta koolitused tudengi litsentsiga üheks aastaks
o https://www.sw.siemens.com/en-US/xcelerator-academy-training/
o https://www.sw.siemens.com/en-US/academic/engineering-student-resources/
o https://training.plm.automation.siemens.com/buy/academic.cfm
o FloEFD
4. AVD füüsikalised ja matemaatilised alused
Voolamise ja soojusülekande protsessid on määratud keeruliste osatuletistega diferentsiaalvõrranditega (Navier–Stokesi võrrandid), mida ei ole võimalik käsitsi lahendada. Seetõttu kasutatakse arvutisimulatsiooni, mis võimaldab:
• saada ligikaudseid lahendusi keerulistele vooluprobleemidele,
• hinnata süsteemi käitumist enne füüsilise prototüübi loomist,
• vähendada katsetuskulusid ja arendusaega.
AVD rakendub väga laialdaselt:
• aerodünaamika (sõidukid, lennukid, reaktiivmootorid),
• energeetika ja masinad (pumbad, ventilaatorid, rootorid),
• elektroonika jahutus,
• soojusülekande analüüs (juhtivus, konvektsioon, kiirgus),
• looduslikud protsessid (konvektsioon, aurustumine).
4.1. AVD füüsikalised alused
AVD tugineb kolmele fundamentaalsele jäävusseadusele, mis kirjeldavad voolise käitumist:
Massi jäävus
Mass ei kao ega teki. Püsiseisundis peab süsteemi sisenev mass olema võrdne väljuva massiga. Valem kokkusurumatu voolise korral: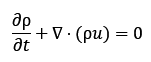
Kui tihedus on konstantne, lihtsustub see kujule: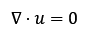
kus u on voolukiiruse vektor.
Impulsi jäävus
Impulss ei kao, vaid muutub välisjõudude mõjul. See on Newtoni II seaduse rakendus voolisele. Navier–Stokesi võrrandi üldkuju: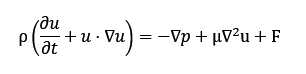
Kus:
· p – rõhk
· m – dünaamiline viskoossus
· F – välisjõud (nt gravitatsioon).
Energia jäävus
Süsteemi sisenev soojus ja genereeritud soojus peavad tasakaalustuma väljuva soojusega.
Üldine energia võrrand:
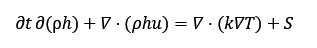
Kus:
· h – entalpia
· k– soojusjuhtivus
· T – temperatuur
· S – soojusallikas.
Need kolm seadust moodustavad aluse Navier–Stokesi võrranditele, mis on osatuletistega diferentsiaalvõrrandid ja kirjeldavad voolamise dünaamikat. Nende lahendamiseks kasutatakse numbrilisi meetodeid, kuna analüütiline lahendus on võimalik ainult väga lihtsustatud juhtudel.
4.2. Soojuslevi mehhanismid AVD-s
Soojuslevi tähendab soojusenergia ülekandumist temperatuurierinevuse tõttu. Erinevalt ühtlasest temperatuurist kehas või süsteemis, kus soojuslevi puudub, toimub energia ülekandumine kolmel viisil: juhtivuslikult, konvektiivselt ja kiirguslikult. FloEFD käsitleb kõiki neid mehhanisme.
Juhtivuslik soojuslevi on soojusenergia ülekandumine läbi tahke aine või paigal seisva voolise. Kui objekti kaks pinda on erineva temperatuuriga, kandub soojus kõrgema temperatuuri pinnalt madalama temperatuuri pinnale.
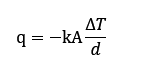
Kus:
· q – soojusvoog [W]
· k – materjali soojusjuhtivus [W/(m·K)]
· A – ristlõike pindala [m²]
· d – objekti paksus [m]
· ΔT – pindade temperatuuride vahe [K].
Konvektiivne soojuslevi toimub voolise liikumise kaudu. Näiteks kui tahke objekt on temperatuuril T1 ja voolis temperatuuril T2, kandub soojus tahkest objektist voolisesse.
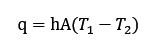
kus
· h– soojusülekande koefitsient [W/(m²·K)]
· A – tahke objekti pindala [m²]
· T– temperatuur [K].
Kiirguslik soojuslevi toimub elektromagnetilise lainena kahe objekti vahel, mille pinnad on erineva temperatuuriga ja mis nii-öelda näevad teineteist. FloEFD-s on saadaval kolm kiirgusmudelit: otsene ülekanne, diskreetne suund (Discrete Ordinates) ja Monte Carlo meetod. Valem (Stefan–Boltzmanni seadus):
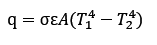
· σ– Stefan–Boltzmanni konstant 5.67×10-8 W/(m2⋅K4)
· ε – pinna emissioonitegur
· A – pindala [m²]
· T – temperatuur [K].
5. AVD matemaatilised alused
Navier–Stokesi võrrand
Navier–Stokesi võrrand on arvutusliku voolise dünaamika keskne matemaatiline mudel. See kirjeldab voolise liikumist, ühendades massi, impulsi ja energia jäävuse seadused ühtseks osatuletistega diferentsiaalvõrrandite süsteemiks. Võrrand on mittelineaarne ja seotud, mis tähendab, et tundmatud (rõhk, kiirus ja temperatuur) mõjutavad üksteist samaaegselt. Üldkujul on impulsi jäävuse võrrand esitatud kujul:
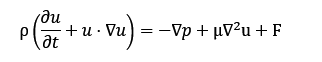
Siin tähistab ρ voolise tihedust, u kiirusvektorit, p rõhku, μ dünaamilist viskoossust ja F välisjõud. Võrrandi vasakul poolel on inertsi ja konvektsiooni liikmed, paremal poolel rõhu gradient, viskoossusjõud ja välised mõjud.
Navier–Stokesi võrrandit ei ole võimalik enamikul juhtudel analüütiliselt lahendada, sest see sisaldab mittelineaarseid ja seotud osatuletisi. Lahendamiseks kasutatakse arvutuslikke meetodeid, mis põhinevad diskretiseerimisel. Diskretiseerimine tähendab, et pidev arvutusruum jaotatakse väikesteks osadeks, mille kohta arvutatakse ligikaudne lahendus.
Lõplike mahuelementide meetod
FloEFD tarkvara rakendab lõpliku mahuelemendi meetodit, mis on üks levinumaid diskretiseerimistehnikaid. Selle meetodi puhul jaotatakse arvutusruum kontrollmahtudeks, mida nimetatakse lahtriteks või võrgusilmadeks. Iga kontrollmahu kohta esitatakse valitsevad võrrandid integraalkujul, mis tagab jäävuse seaduste täitmise lokaalselt. Näiteks üldine integraalkujuline vorm on:
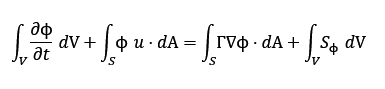
kus
ϕ – üldine suurus (rõhk, temperatuur, kiiruskomponent),
V – kontrollmaht,
S – pind,
Γ – difusioonikoefitsient,
Sϕ – allikaterm.
Siin on ϕ üldine suurus, mis võib tähistada rõhku, temperatuuri või kiiruskomponenti, V kontrollmaht ja S selle pind. Vasakul poolel on ajamuutus ja konvektsioon, paremal poolel difusioon ja allikaterm. FloEFD-s paiknevad kontrollmahud geomeetria sees ja piirpindade lähedal. Üldiselt kasutatakse paralleelseid risttahukaid. Piirpindade lähedal, kus voolise ja tahke keha kontakt on oluline, kasutatakse keerukama kujuga hulktahukaid (polüeedreid). Põhimuutujad viidatakse kontrollmahu massikeskmetele, mis lihtsustab arvutust ja tagab täpsuse.
Lõpliku mahu meetodi eelis on see, et see säilitab füüsikaliste suuruste jäävuse igas kontrollmahus, mis on kriitiline insenerisimulatsioonide usaldusväärsuse jaoks. FloEFD integreerib selle meetodi CAD-keskkonda, võimaldades inseneridel luua võrgustiku automaatselt ja määrata piiritingimused otse geomeetriale.
6. Võrgustiku loomine ja keha jaotamine kontrollmahtudeks
Numbrilise lahenduse eelduseks on arvutusruumi jaotamine väikesteks osadeks, mida nimetatakse kontrollmahtudeks. FloEFD-s realiseeritakse see võrgustiku abil, mis koosneb lahtritest ehk võrgusilmadest. Need lahtrid katavad kogu arvutusruumi, sealhulgas voolise ja tahke keha piirkonnad. Võrgustiku kvaliteet määrab simulatsiooni täpsuse ja arvutusaja. Joonis 1 kujutab paksuseinalise toru ristlõiget, millele on laotatud kartesiaanvõrgustik, mille risttahukad on küljepikkusega 15;10;5 ja 2,5.

Joonis 1. Kartesiaanvõrgustik erinevate lahtrisuuruste korral.
Oluline FloEFD tehnoloogia on vedeliku-tahke aine piirpindadega lahtrid (varasemalt nimetatud osalisteks lahtriteks). Need tekivad seal, kus lahter lõigatakse kaheks, üks osa jääb tahkesse kehasse, teine voolisesse. Piirpindadega lahtrid võimaldavad täpselt kirjeldada voolise ja tahke keha koostoimet ilma, et oleks vaja luua väga tihedat võrgustikku seina lähedal. FloEFD rakendab muudetud seinafunktsioone, mis haaravad piirikihi mõju automaatselt. Erinevalt klassikalistest AVD meetoditest ei pea kasutaja määrama piirikihi paksust ega lahtreid, sest see toimub automaatselt, tuginedes füüsikalistele ja empiirilistele mudelitele.
Lisaks pakub FloEFD lahenduspõhist võrgustiku täpsustamist. See funktsioon peatab analüüsi teatud etapis, hindab voolu gradientide jaotust ning täpsustab võrgustikku seal, kus gradientid on suurimad. See on eriti kasulik keerukates olukordades, näiteks lööklainete või aerodünaamiliste nähtuste korral, kus kriitiliste piirkondade asukohta on raske ette ennustada. Lahenduspõhine täpsustamine toimub automaatselt ja vähese kasutaja sisendiga, mis tähendab, et täpsus paraneb minimaalse arvutusaja kasvuga.
FloEFD võimaldab ka kasutajal ennetavalt täpsustada võrgustikku piirkondades, kus on teada kitsad kanalid, radiaatorid või ventiili avad. Selline lokaalne täpsustamine koos automaatse lahenduspõhise täpsustamisega tagab, et simulatsioon on täpne ja arvutusressursid on optimaalselt kasutatud.
6.1. Võrgustik FloEFD-s
Numbrilise lahenduse eelduseks on geomeetria jaotamine väikesteks osadeks ehk lahtriteks, kus lahendatakse Navier–Stokesi võrrandid. FloEFD kasutab lõplike mahuelementide meetodit (LMM), mis tähendab, et iga lahtri kohta arvutatakse valitsevad võrrandid integraalkujul. Lahtrite massikeskmetes paiknevad põhimuutujad: rõhk, temperatuur, kiiruskomponendid ja turbulentsiparameetrid. Lahtri pindadel aga arvutatakse voolude ja soojusvoogude integraalsed väärtused.
FloEFD rakendab kartesiaanvõrku, mis koosneb risttahukakujulistest lahtritest. Kartesiaanvõrk on valitud selle lihtsuse, kiiruse ja stabiilsuse tõttu. See vähendab arvutusvigu ja võimaldab regulaarset täpsustamist. Võrgustiku täpsustamine toimub oktaarse jaotuse abil, kus iga lahter jagatakse vajadusel kaheks, neljaks või enamaks osaks.
Kartesiaanvõrgu eelisteks on:
- Lihtsus ja stabiilsus - Kartesiaanvõrk on geomeetriliselt regulaarne, mis muudab algoritmid stabiilseks ja vähendab arvutusvigu. Regulaarne struktuur võimaldab täpset kontrolli lahtrite suuruse ja jaotuse üle, mis on oluline koondumise (konvergentsi) saavutamiseks.
- Väiksem arvutuslik viga - Kartesiaanvõrk minimeerib truncation error’i ehk lõikeviga, mis tekib osatuletiste diskretiseerimisel. Kuna lahtrid on ühtlased, on arvutuslik skeem lihtsam ja täpsem võrreldes ebakorrapäraste võrkudega.
- Kiirus ja efektiivsus - Kartesiaanvõrk võimaldab kiiret automaatset genereerimist ja täpsustamist. FloEFD kasutab oktaarset täpsustamist, kus iga lahter jagatakse vajadusel kaheks, neljaks või enamaks osaks. See protsess on regulaarne ja prognoositav, mis vähendab arvutusaega ja hoiab võrgustiku loogilise struktuuri.
- Lihtne täpsustamine kriitilistes piirkondades - Kartesiaanvõrk sobib hästi lahenduspõhise täpsustamise jaoks. FloEFD tuvastab voolu gradientide põhjal piirkonnad, kus on vaja tihedamat võrku, ja rakendab täpsustamist automaatselt. Kuna võrk on regulaarne, saab täpsustamist teha lokaalselt ilma kogu mudelit ümber arvutamata.
- Piirpindade käsitlus - Kuigi kartesiaanvõrk ei järgi täpselt keeruka geomeetria kontuure, kompenseerib FloEFD seda piirpindadega lahtrite tehnoloogiaga. Lahtrid, mis lõikuvad tahke keha ja voolise vahel, jagatakse osadeks, mis jälgivad geomeetria kuju. See võimaldab täpset piirikihi simulatsiooni ilma väga tiheda võrgustiku vajaduseta.
- Väiksem võrgustiku arvutuskoormus - Kartesiaanvõrk saavutab suure täpsuse väiksema lahtrite arvuga võrreldes tetraeedriliste või keha-järgivate võrkudega. See tähendab lühemat arvutusaega ja väiksemat mälukasutust, mis on oluline inseneritöö praktilises kontekstis.
Naaberlahtrite täpsustamise tase võib erineda maksimaalselt ühe astme võrra, mis tagab stabiilse ja prognoositava võrgustiku. FloEFD lubab kuni üheksa täpsustustaset, mis võimaldab väga detailset lahendust kriitilistes piirkondades.
Allpool on joonisel 1 toodud mõned näited võrgustiku täpsustamisest voolukriitilistes piirkondades ning kitsastes kanalites:
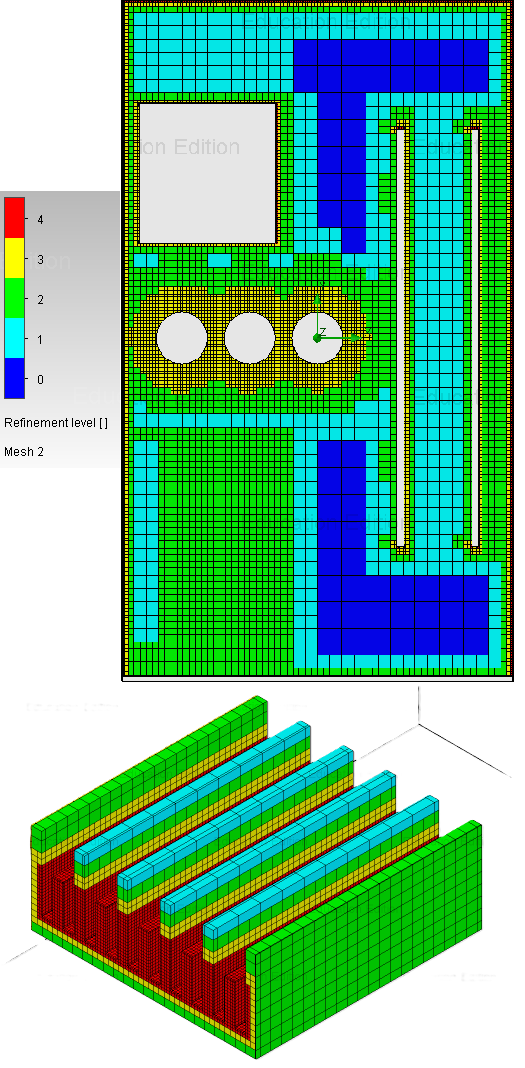
Joonis 1. Võrgustik ja selle täpsustused trükkplaadil voolukriitilistes kohtades ja radiaatori kitsastes piludes koos värviskaala legendiga.
Nagu jooniselt 1 ja 2 selgub, siis võrgustikus säilib lahtrite üldine mastaap. Täpsustamiseks on vaja vaid lahter jagada sama mastaabiga risttahukateks. joonisel 1 kasutatud värviskaalast ja joonisel 2 kujutatud võrgustikust selgub, et kõrvutiolevad lahtrid saavad erineda maksimaalselt vaid ühe taseme võrra.
Võrgustikus esineb kolme tüüpi lahtreid:
- Voolise lahtrid, mis asuvad täielikult vedeliku või gaasi piirkonnas.
- Tahke keha lahtrid, mis asuvad täielikult tahkes piirkonnas.
- Piirpindadega lahtrid, mis lõigatakse kaheks osaks – üks osa jääb voolisesse, teine tahkesse kehasse.
Need piirpindadega lahtrid on FloEFD tehnoloogia tuum, sest need võimaldavad täpselt kirjeldada voolise ja tahke keha koostoimet ilma väga tiheda võrgustiku vajaduseta. Piirpindadega lahtrites rakendatakse muudetud seinafunktsioone, mis simuleerivad piirikihi nähtusi automaatselt.
FloEFD suudab ühes lahtris käsitleda kuni 36 erinevat materjali, kuigi soovitatav on piirduda kümnega. Piirpindadega lahtrid võivad sisaldada mitu kontrollmahtu (nii tahke keha kui ka voolis ühes lahtris)– tavaliselt kuni neli, et säilitada täpsus ja arvutuskiirus. Näiteks on soovitatav, et ribide kitsas vahe sisaldaks vähemalt nelja lahtrit, millest kaks on täielikult voolises ja kaks piirpindadega. Kui tegemist on keerukama analüüsiga, ei tohiks ühe lahtris olla üle 2 kontrollmahu.
Alltoodud joonisel 2 on kujutatud pealtvaates eelnevalt kolmemõõtmelisena kujutatud kaks radiaatoriribi otsa, mille kontuure tähistab punane joon.
- Sinisega on tähistatud mõned piiripindade lahtrid.
- Halliga on tähistatud mõned voolise lahtrid
- Valgega on tähistatud mõned tahked lahtrid

Joonis 2. Radiaatori ribide võrgustiku jaotus.
jooniselt 2 on näha, et kitsas kanal kahe ribi vahel on täpsustatud rohkem kui on miinimumnõue, sest kanali ristlõikes on voolise lahtreid 4 ja piirpinna lahtreid 2. See võib olla mõnel juhul vajalik, kuid mitte alati.
Oluline uuendus FloEFD võrgustustehnoloogias on geomeetria täpne lõikamine. Varasemates versioonides kasutati cut cell meetodit, mis lihtsustas geomeetria nurki ja võis põhjustada täpsusvigu.
Alates uuemast versioonist rakendatakse real geometry meetodit, mis arvestab mudeli tegelikke nurki ja servasid, vähendades vajadust liigse täpsustamise järele ja tagades suurema täpsuse väiksema lahtrite arvuga.
7. FloEFD võimekus ja võimalused
Simcenter FloEFD on arvutusliku voolise dünaamika (AVD) tarkvara, mis on loodud inseneridele, et viia simulatsioonid otse CAD-keskkonda. Selle peamine tugevus seisneb seitsmes võtmetehnoloogias, mis muudavad analüüsi kiireks, täpseks ja kasutajasõbralikuks.
Täielik CAD-integratsioon
FloEFD on tihedalt integreeritud Solid Edge’i ja teiste MCAD-süsteemidega. See tähendab, et simulatsioonid viiakse läbi otse projekteerimiskeskkonnas, kasutades sama geomeetriat. Mudeli muudatused kajastuvad koheselt simulatsioonis ja vastupidi, mis välistab vajaduse geomeetria konverteerimiseks ja vähendab vigade riski. Kasutajal on simulatsiooni ajal ligipääs kõigile CAD-funktsioonidele, sealhulgas mõõtmetele ja abipindadele. See tagab mudelite ja simulatsioonide sünkroonsuse kogu tootearenduse vältel.
Automaatne võrgustiku loomine
FloEFD tuvastab automaatselt voolise ja tahke keha piirpinnad ning genereerib sobiva võrgustiku ilma käsitsi sekkumiseta. Tarkvara korrigeerib kattuvad geomeetriad ja arvestab detailide asendeid, näiteks ventiilide erinevaid positsioone. Võrgustiku tihendamist või harvendamist saab juhtida automaatselt või lokaalselt täpsustada. See vähendab ülesseadmise aega ja kõrvaldab vajaduse süvitsi AVD teadmiste järele.
Kasutajaliides
FloEFD pakub juhendatud seadistusabilist (Project Wizard), mis viib kasutaja läbi 6–7 sammu, et luua simulatsiooniprojekt. Liides võimaldab tulemuste analüüsi tabelite, graafikute ja visualisatsioonide kujul ning ekspordi MS Office’i vormingutesse (Excel, Word). See lihtsustab dokumentatsiooni loomist ja vähendab seadistamise aega.
Täiustatud turbulentsimudel
FloEFD kasutab unikaalset modifitseeritud k-ε mudelit laminaarse, ülemineku ja turbulentse voolu modelleerimiseks. Voolu režiim määratakse automaatselt, kuid kasutajal on võimalus seda käsitsi muuta. See lähenemine vähendab seadistamise keerukust ja suurendab täpsust võrreldes traditsiooniliste meetoditega.
Muudetud seinafunktsioon piirikihtidele
FloEFD rakendab automaatset seinalähedast modelleerimist, mis ei sõltu võrgustiku tihedusest. Piirikihi nähtused simuleeritakse füüsikaliselt korrektselt nii voolamise kui soojuslevi puhul. Kitsad kanalid ja kriitilised piirkonnad haaratakse automaatselt täpse võrguga, ilma et kasutaja peaks piirikihi paksust määrama. See vähendab katse-eksituse meetodil seadistamise vajadust.
Automaatne lahenduse koondumine
FloEFD-l on tugev konvergentsikäitumine, mis tähendab, et lahendus saavutatakse nii jämeda kui peene võrguga ilma täiendava numbrilise difusioonita. See kõrvaldab korduvate jooksude vajaduse ja võimaldab mitme variandi analüüsi lühikese ajaga. Kui lahendus ei koondu, on probleem tavaliselt seadistuses, mitte algoritmis.
Mitme variandiga ja optimeerimisanalüüs
FloEFD sisaldab parameetrilist uuringu funktsiooni, mis võimaldab mis-juhtub-kui analüüse ja optimeerimist. Projekti kloonimise abil saab kiiresti luua uusi juhtumeid, säilitades kõik piiritingimused ja seadistused. Tarkvara toetab MCAD konfiguratsioone ja eksemplare, mis teeb disaini iteratsioonid kiireks ja tõhusaks.
7.1. FloEFD võimekus
FloEFD on loodud laia valiku voolamise ja soojuslevi nähtuste simuleerimiseks, pakkudes inseneridele tööriista, mis katab nii lihtsad kui keerukad olukorrad. Tarkvara suudab lahendada nii väliseid kui sisemisi voolusid, sealhulgas statsionaarsed ja üleminekuvoolud. Toetatud on kokkusurutava gaasi, vedeliku ja kokkusurumatu voolise simulatsioonid, samuti vaba, sunnitud ja segakonvektsioon. Piirkihid ja seina karedusest tulenevad efektid arvestatakse automaatselt, mis tagab täpsuse seinalähedastes piirkondades.
FloEFD käsitleb laminaarseid ja turbulentseid voolusid ning võimaldab analüüsida mitmekomponendilisi vooliseid ja tahkeid kehi. Soojuslevi arvutatakse voolistes, tahketes ja poorsetes keskkondades, sealhulgas isotroopse, ühesuunalise, kahe telje suunalise ja anisotroopse soojusjuhtivusega materjalides, näiteks trükkplaatides ja radiaatorites. Tarkvara toetab mitte-Newtoni vedelikke, reaalseid gaase ja kahefaasilisi voolusid, sealhulgas vedeliku-gaasi-auru segusid ja osakeste liikumist.
Lisafunktsioonid hõlmavad suhtelise õhuniiskuse modelleerimist, pöörlevate pindade ja detailide simulatsiooni (ventilaatorid, pumbad), kavitatsiooni kokkusurumatu vee vooludes ning tasakaalulist ruumala kondenseerumist, mis on oluline soojusvahetites ja auruturbiinides. FloEFD suudab arvutada pindkondensatsiooni, jää moodustumist ja sulamist, samuti vaba pinna liikumist vedeliku ja gaasi vahel, näiteks loksuv paak või merepind. Lisaks on võimalik hinnata veeauru imendumist tahketesse ainetesse, mis on oluline udu tekke ja niiskuse prognoosimisel.
Tarkvara pakub ka laiaribalise müra analüüsi, mis põhineb isotroopse turbulentsi poolt genereeritud akustilisel võimsustasemel vastavalt Proudmani definitsioonile.
Siiski tuleb arvestada piirangutega: FloEFD ei toeta liikuvat võrgustikku lineaarsete liikumiste jaoks (nt , lineaartõukurid ja kolvid), kuid pöörlevad võrgustikud on täielikult toetatud. Voolise ja konstruktsioonide koostoimet ei simuleerita otse, kuid tulemusi saab eksportida konstruktsioonianalüüsi tööriistadesse.
7.2. Simulatsiooni eesmärgid
Enne AVD simulatsiooni käivitamist tuleb inseneril selgelt mõista, mida ta soovib simulatsioonist saada. FloEFD-s nimetatakse neid huviparameetreid projekteerimise eesmärkideks (engineering goals). Eesmärgid ei ole pelgalt tulemuste kuvamise vahend, vaid neil on kolm olulist rolli:
Koonduvuse kontroll- FloEFD kasutab eesmärke, et hinnata, kas lahendus on jõudnud püsiseisundisse. Kui eesmärgid on määratud koonduvuse kriteeriumidena, jätkab solver arvutamist seni, kuni nende väärtused stabiliseeruvad. See on täpsem kui vaikimisi iteratsioonide arv, sest koonduvus sõltub füüsikaliste parameetrite stabiilsusest.
Simulatsiooni jälgimine-Eesmärgid võimaldavad arvutuse käigus jälgida olulisi parameetreid (nt rõhk, temperatuur, kiirus) kindlates punktides, pindadel või kogu arvutuspiirkonnas. See aitab tuvastada, kas mudel käitub ootuspäraselt.
Järeltöötlus ja tulemuste analüüs-Eesmärgid lihtsustavad tulemuste analüüsi, sest FloEFD salvestab nende väärtused iga iteratsiooni kohta. Näiteks saab kontrollida rõhukadu, Reynoldsi arvu või soojuslevi intensiivsust ilma täiendavate käsitsi arvutusteta.
Eesmärkide tüübid FloEFD-s
Globaalne eesmärk- Füüsikaline parameeter, mis arvutatakse kogu arvutuspiirkonnas. See arvestab kõiki võrgu elemente mudelis ega ole seotud komponendi, pinna ega punktiga. Globaalset eesmärki kasutatakse, kui soovid jälgida üldisi tulemusi, et veenduda, et kõik tundub mõistlik. Näited: min/max kiirus, rõhk, temperatuur.
Punktieesmärk- Seotud kindla koordinaadiga või geomeetrilise punktiga. Punktieesmärkide rakendused on näiteks termiliselt koormatud asukoht, kiirus punktist ülesvoolu, rõhk või tihedus. Näited: p(x,y,z), ρ(x,y,z), v(x,y,z).
Pindade eesmärk- Rakendatakse valitud piirpinnale (pindadele) (nt sisselaske või väljalaske ava). Näited: keskmine rõhk, massvoolu keskmine, soojuslevi.
Ruumala eesmärk- Rakendatakse kindlale kehale või mahule. Näited: maksimaalne temperatuur, kontsentratsioon.
Võrrandi eesmärk- Kasutab teisi eesmärke ja sisendtingimusi valemi koostamiseks. Tüüpilised rakendused on rõhukadu, Reynoldsi arv, tõste- ja takistuskoefitsiendid, pumba efektiivsus jne. Näide: rõhukadu Δp = pin − pout.
Kui kasutad eesmärke koonduvuseks, tähistatakse neid musta ja kollase lipuga. Kui aga kasutad neid jälgimiseks, tähistatakse neid punase ja kollase lipuga.