Cantera rakendusvõimalused koos näidetega
| Õpikeskkond: | Eesti Maaülikooli Moodle |
| Kursus: | Simulatsioonid |
| Raamat: | Cantera rakendusvõimalused koos näidetega |
| Printija: | Külaliskasutaja |
| Kuupäev: | esmaspäev, 26. jaanuar 2026, 02.18 AM |
1. Termodünaamika rakendamine simulatsioonis
Keemiline tasakaal
Keemiline tasakaal on olek, kus süsteemi lähteainete ja saaduste kogused ei muutu ajas, sest päri- ja vastassuunaliste reaktsioonide kiirused on võrdsed. Teisisõnu, netoreaktsioonikiirus on null suletud süsteemis.
Kuidas Canteras tasakaalu arvutada?
Tasakaalu leidmiseks kasutatakse funktsiooni equilibrate(), mis kuulub termodünaamika faasi (Solution/ThermoPhase) meetodite hulka.
>> set(g,'T',1500.0,'P',oneatm,'X','CH4:1,O2:2') [23]
>>equilibrate(g,'TP') [23]
Tähis „g“ vastab GRI30 ideaalse gaasi kogumikule, „T“ on kindel temperatuur, „P“ on kindel rõhk, „X“ tähendab, et muudetakse mooli fraktsiooni. Temperatuuri ja rõhu asemel võib määrata ka temperatuuri ja mahu, entalpiat ja rõhu, entroopiat ja mahu, siseenergiat ja mahu ning siseenergiat ja rõhu.
Tulemuste kontrollimiseks tuleb sisestada järgnevalt toodud kood. Tulemustes peab kontrollima, et vastassuunaliste reaktsioonide kiirused võrduvad nulliga:
Tulemus näitab, et vastassuunaliste reaktsioonide kiirused võrduvad nulliga ümbritsetud punasega).
Näide (GRI30 ideaalgaasi faas):

Tulemuseks on:
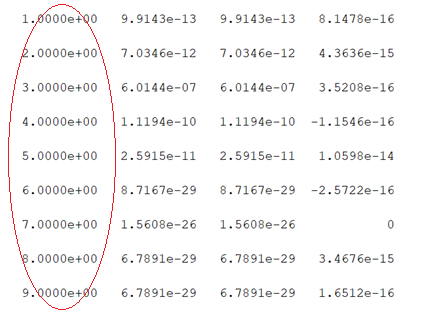
Tulemus näitab, et vastassuunaliste reaktsioonide kiirused võrduvad nulliga (ümbritsetud punasega).
2. Kineetika rakendused simulatsioonis
2.1. Stöhhiomeetrilised koefitsiendid
Stöhhiomeetria kirjeldab, kui palju ja missuguses suhtes osalevad ained keemilises reaktsioonis ning millised on saaduste kogused. Reaktsioonivõrrandi stöhhiomeetrilised koefitsiendid määravad reaktiivide ja toodete moolsuhted, mis on aluseks nii massibilansi koostamisel, kiirusvõrrandite kirjutamisel kui ka reaktsioonivõrkude simulatsioonis.
Üldkujul võib reaktsiooni i kirjutada:

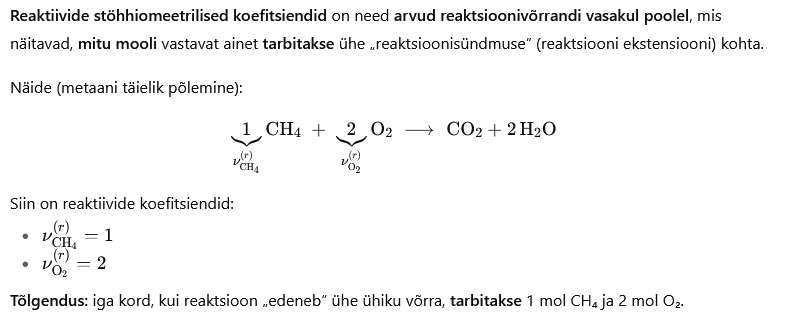
Kuidas Canteras stöhhiomeetriat lugeda?
Cantera pakub otsejuurdepääsu reaktiivide, toodete ja neto koefitsientidele. Nimekujud võivad versiooniti erineda (eriti MATLAB-i liideses), seega on toodud nii “klassikalised” kui ka uuemad nimetused.
MATLAB (olenevalt versioonist):
- stoich_r(g, species, rxns) või reactantStoichCoeffs(g) → reaktiivide koefitsiendid,
- stoich_p(g, species, rxns) või productStoichCoeffs(g) → saaduse koefitsiendid,
- stoich_net(g, species, rxns) või arvuta ise productStoichCoeffs(g) - reactantStoichCoeffs(g).
Kus „a“ on kindlate omadustega valitud katsetatav element (kogumik), „species“ on mooli(X) -või massifraktsioonid(Y) ning „rxns“ on maatriksi element (k,i), „k“ on kogumiku sees olevate elementide arv ning „i“ on reaktsiooni arv.
Argumendid:
- g – Cantera faasiobjekt (nt Solution('gri30.yaml')),
- species – valikulised liigiindeksid (nt [] või 1:nspecies),
- rxns – valikulised reaktsiooniindeksid (nt [] või 1:nreactions).
Kui species ja rxns jätad täitmata, tagastatakse täismaatriks mõõtudega (liigid × reaktsioonid) (sageli hõre maatriks).
Näidis, reaktiivide koefitsientidest (g = GRI 30).
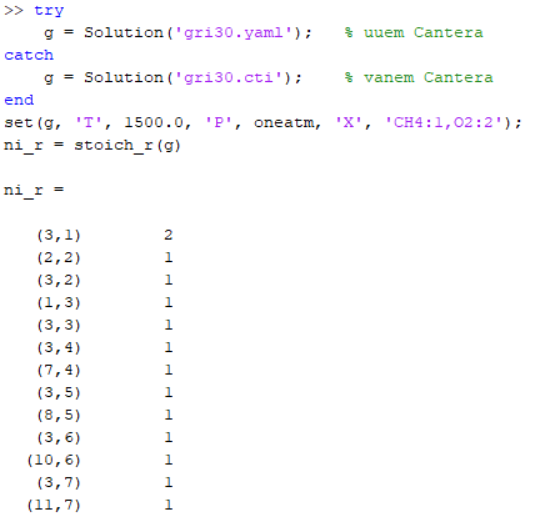
Täpsustuseks: näites toodud koodi osa set()… sisaldab lõpus osasid, CH4:1,O2:2. numbrid metaani ja hapniku taga iseloomustab nende osakaalu reaktsioonis. Üldiselt arvestatakse neid moolides.
Proovida ka:
>> set(g,'T',2000,'P',oneatm,'X',ones(nSpecies(g),1));
>> nu_r = stoich_r(g)
nu_r =
Antud koodis:
- annab kõikidele liikidele võrdsed mooliosad;
- see ei muuda steöhhiomeetriat;
- steöhhiomeetria tuleb mehhanismi failist, mitte olekust.
Eeltoodud tulemused on jaotunud veergudeks, kus esimene veerg on liik (mis liiki reaktsiooniga on tegemist, cantera sisene) ja teine veerg on reagendi koefitsient: Järgnev näide on Cantera tulemuste näide.
|
Liik |
Reagentikoefitsient |
|
O |
1 |
|
H₂ |
1 |
|
OH |
0 (sest OH on saadus, mitte reagent) |
|
H |
0 |
|
kõik ülejäänud |
0 |
Reaktsioonide kiirused
Meetodeid mida kasutatakse on kokku kolm:
- rop_f(a) – kõikide reaktsioonide edasiliikumise kiirus;
- rop_r(a) – kõikide reaktsioonide tagasiliikumise kiirus;
- rop_net(a) – (edasiliikumine – tagasiliikumine).
Kus „a“ on katsetav element (kogumik). Koodi näidis on toodud järgnevalt:
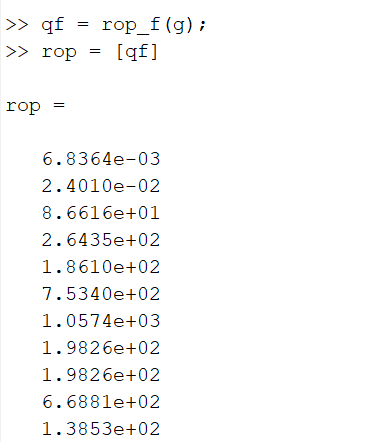
Reaktsioonide edasiliikumise arvutamise näidiskood (g = GRI 30). Pane tähele, et sa seaksid keskkonnaparameetrite puhul temperatuuriks 2000K. Vastasel juhul on tulemused alguses „0“.
Lisaks, on võimalik luua graafik, et illustreerida reaktsioonide edenemise kiirust. Selle jaoks tuleb sisestada käsk:
>> figure(1);
>>bar(rop);
>>legend('Edasiliikumine');
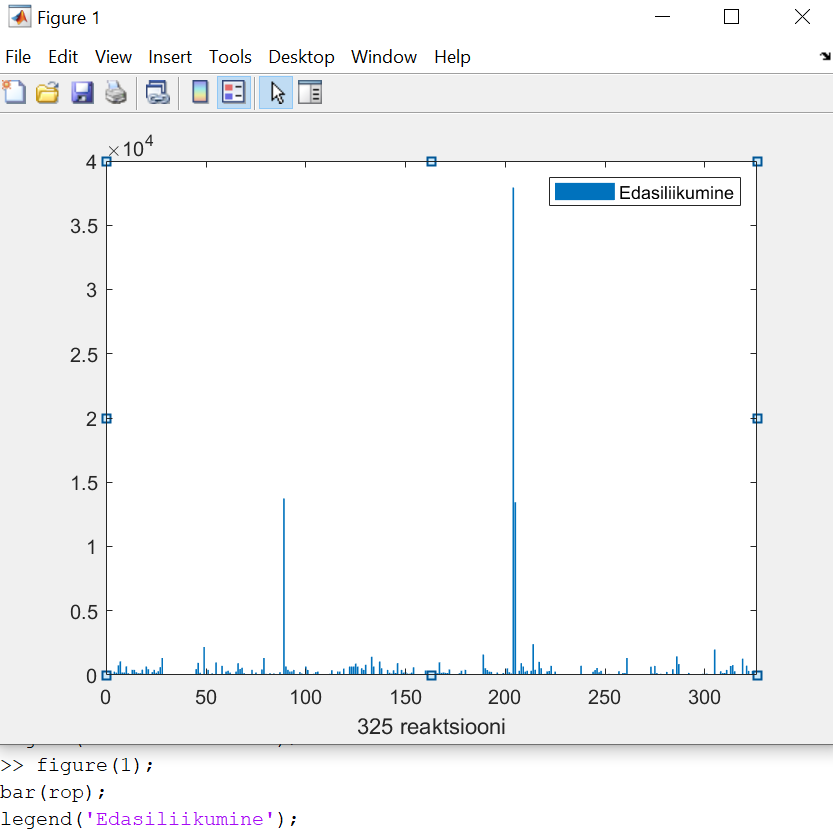
Loodud graafik, reaktsioonide edenemise kiirus. Enamikul reaktsioonidel on tulp null. See on normaalne, sest GRI30 mehhanismis on 325 reaktsiooni, kuid näites kasutatud segus on:
- ainult mõned liigid on reaalselt olemas;
- paljud reaktsioonid vajavad CO, CO₂, OH, HO₂, H₂O, CH₃, N₂ jne;
- kui mõni reagent puudub → reaktsiooni kiirus = 0.
Seepärast on enamus tulpasid null-tasemel.
2.2 Erinevate kogumike/elementide reaktsioonide tekkimise ja lagunemise näitajad
Kasutatavaid meetodeid on kokku kolm:
- creationRates(a) – tekke kiirus;
- destructionRates(a) – lagunemise kiirus;
- netProdRates(a) – netotootmise kiirus (nähtav).
Kus „a“ on katsetatav element (kogumik). Koodi näidis:
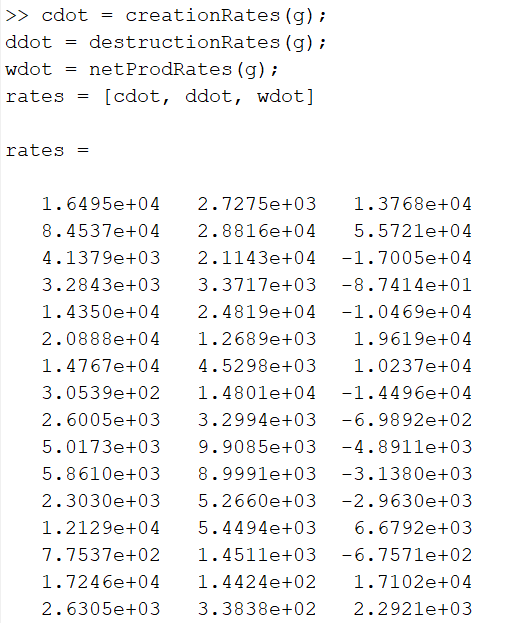
Näidis kõikide reaktsioonide tekkimise, lagunemise ja neto kiirustest (g = GRI 30).
Järgneval joonisel on näha, et esimene tulp näitab reaktsioonide tekkimise kiirust, teine tulp näitab lagunemise kiirust ning kolmas tulp näitab netotootmise kiirust ehk mis reaalselt reaktsiooni loomise käigus jäi (peale lagunemist). Nende reaktsioonide näitude abil saab luua graafiku ning võrrelda tulemusi:
>> figure(2);
>> bar(rates);
>> legend('Tekke kiirus','Lagunemise kiirus','Neto kiirus');
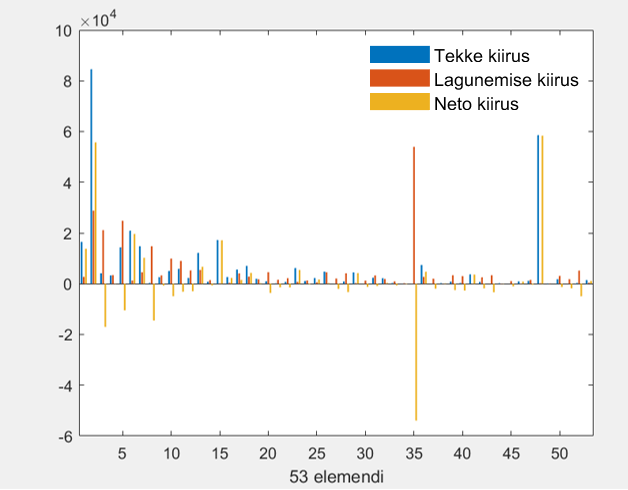
Reaktsioonide tekke, lagunemise ja neto kiirus. Analüüsi joonist, ning võrdle tekke ning lagunemiskiiruseid. Uuri välja, mis on reaktsiooni tekkekiirus, lagunemise kiirus ning netokiirus.
2.3. Keemiliste reaktsioonide rakendamine simulatsioonis
Erinevad võimalused, kuidas näha mingi kindla ainete kogumiku reaktsioone. Näidiseks on valitud g = GRI 30 (53 liikide kogumik). Selleks, et näha konkreetselt viiendat reaktsiooni tuleb sisestada käsk:
>> e8 = reactionEqn(g,5)
Vastuseks tuleb:
e8 =
'H2O2 + O <=> HO2 + OH' Samuti võib valida reaktsioone ka mingis kindlas vahemikus, näidis (GRI 30 reaktsioonid vahemikus 1-8).
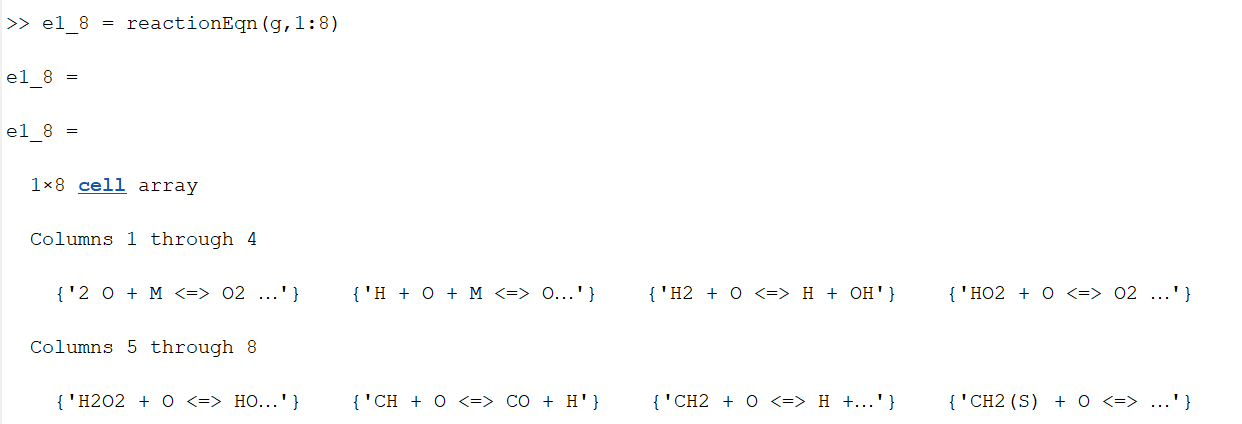
Joonisel on näha GRI30 kogumiku elementide reaktsioonid vahemikus 1- 8 , juhul kui on soov näha reaktsioone näiteks vahemikus 1-20, siis koodi esimeses reas tuleb kirjutada mitte 1:8, vaid 1:20.
Selleks, et saaks näha kõikide ainete omavahelist reaktsioone tuleb sisestada käsk:
>> eqs = reactionEqn(g)
Programm väljastab tulemuse:
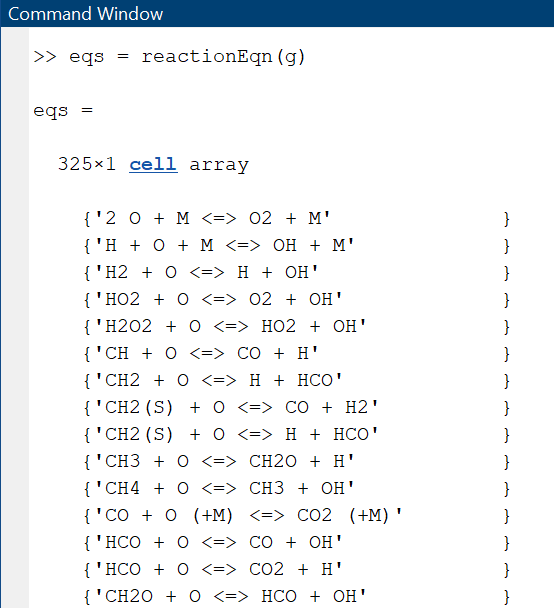
Programmi poolt väljastatud tulemus (esimesed 15 reaktsiooni, kokku näitab 325).
Vedelike/gaaside ülekandeomadused
Selles osas on toodud välja erinevad funktsioonid, mida kasutatakse transportimise omaduste välja arvutamiseks. On oluline teha kindlaks millist elementide kogumiku hakatakse katsetama. Praegu kasutatakse kahte põhilist mudelit ning mõlemad põhinevad kineetilise teooria väljenditel. Esimeses mudelis on mitmekomponendiline koostis ning teine mudel on lihtsustatud, kuna seal kasutatakse ainult 1-3 liikide segudega seotud väljendeid, et keskmistatud koostis.
Esimene mudel:
>> g1 = GRI30('Multi')
Teine mudel:
>> g2 = GRI30('Mix')
Omadused, mida saab leida mõlemal mudelil:
Viskoossus
>> visc = [viscosity(g1), viscosity(g2)]
visc =
9.0002e-06 9.0002e-06
Soojusjuhtivus
>> lambda = [thermalConductivity(g1), thermalConductivity(g2)]
lambda =
1.8691e-01 1.8679e-01
Binaarsed difusioonikoefitsiendid
>> bdiff1 = binDiffCoeffs(g1)
>> bdiff2 = binDiffCoeffs(g2)
Näidis, kuidas antud kood näeb välja MatLabi käsuaknas:
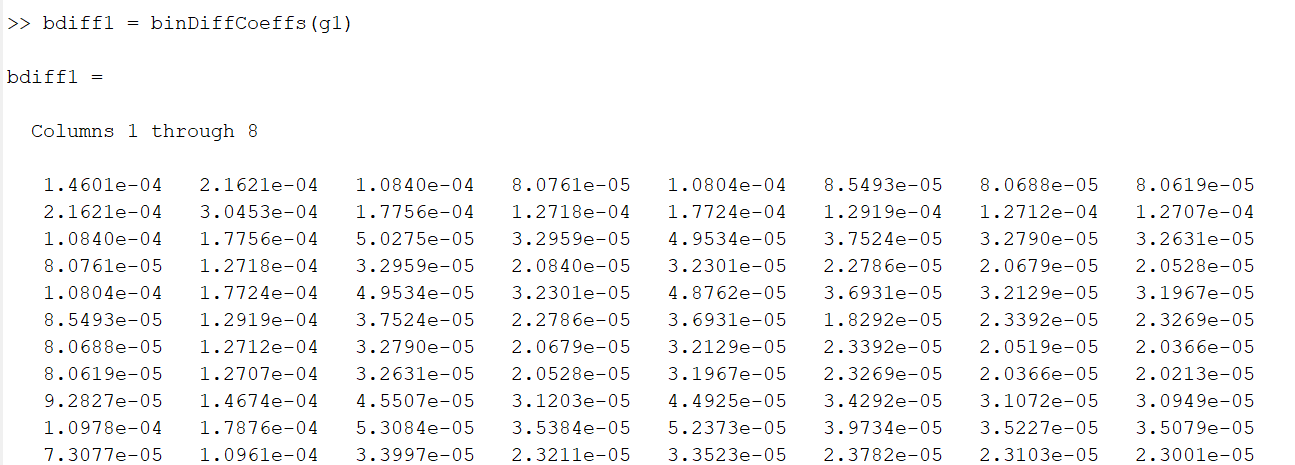
Esimese mudeli binaarsed difusioonikoefitsiendid.
Segukeskmised difusioonikoefitsiendid
>> dmix2 = mixDiffCoeffs(g1)
>> dmix1 = mixDiffCoeffs(g2)
MatLabi käsuakna vaade:
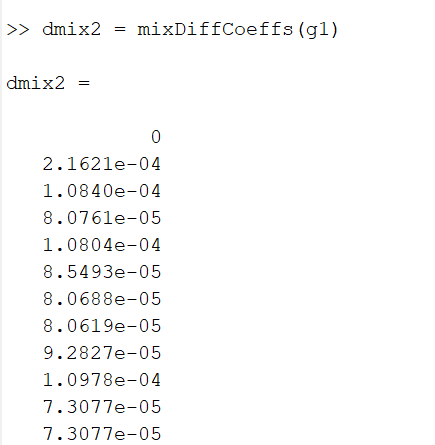
Esimese mudeli segukeskmised difusioonikoefitsiendid.
Omadused, mida saab leida ainult esimesel mudelil:
Mitmekomponendilised difusioonikoefitsiendid
>> dmulti = multiDiffCoeffs(g1)
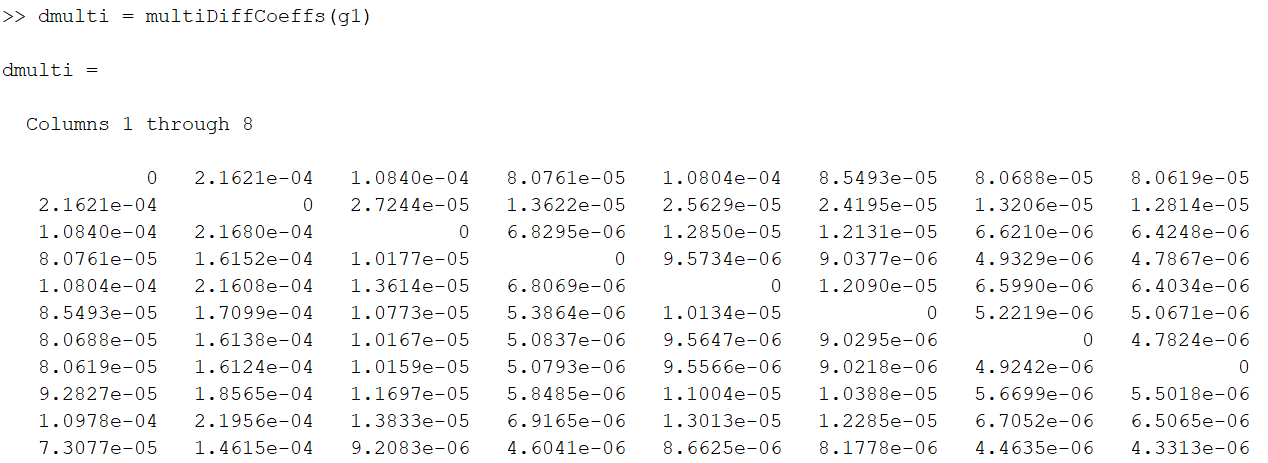
Esimese mudeli mitmekomponendilised difusioonikoeditsiendid.
Käsk multiDiffCoeffs(g1) tagastab mitmekomponendilise difusioonikoefitsientide maatriksi, mille iga element Dij, kirjeldab liigi i difusioonivoolu tundlikkust liigi j kontsentratsioonigradientide suhtes. Maatriks on suurusega liikide arv × liikide arv (nt 53×53 GRI30 korral) ja annab täieliku Maxwell–Stefani mudeli koefitsiendid. Seega tabel ei näita üksikuid difusioonikoefitsiente, vaid kõigi liikide omavahelisi difusioonisuhteid.
Termilise difusiooni koefitsiendid
>> dt = thermalDiffCoeffs(g1)
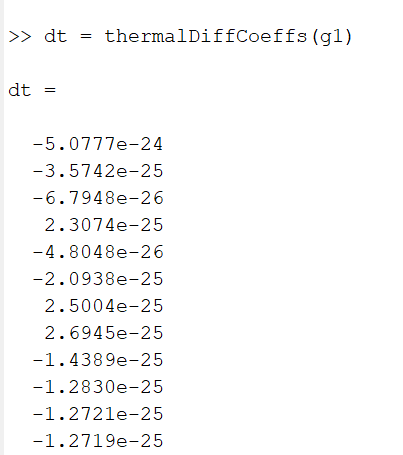
Esimese mudeli termilise difusiooni koefitsiendid.