Cantera-tarkvara teoreetilised alused
| Õpikeskkond: | Eesti Maaülikooli Moodle |
| Kursus: | Simulatsioonid |
| Raamat: | Cantera-tarkvara teoreetilised alused |
| Printija: | Külaliskasutaja |
| Kuupäev: | esmaspäev, 26. jaanuar 2026, 02.18 AM |
Sisukord
- 1. Cantera programmi tutvustus
- 2. Simulatsioonitarkvara teoreetilised alused – parandatud ja täpsustatud
- 2.1. Termodünaamika
- 2.1.1 Entalpia
- 2.1.2. Siseenergia
- 2.1.3. Termodünaamika I seadus
- 2.2. Keemiline tasakaal
- 2.2.1. Elementaarreaktsioon
- 2.2.2. Mitteühtlane, gaasifaasi reaktsioon (kolmekehaline reaktsioon)
- 2.2.3. Pinnareaktsioonid
- 2.2.4. Kleepumisreaktsioonid
- 2.3. Ülekandeprotsessid (transport properties)
- 2.3.1. Ülekandemudel: multi
- 2.3.2. Ülekandemudel: segu (mix)
- 2.4. Difusiooni koefitsient
- 2.5. Reaktorid
- 2.5.1. Reaktorite seinad (walls)
- 2.5.2. Mahu reaktor
- 2.6. Leegid
1. Cantera programmi tutvustus
Cantera on tarkvaratööriistade kogum, millega saab lahendada mitmesuguseid probleeme, mis on seotud keemilise kineetika, termodünaamika ja ainete ülekandeprotsessidega. Täpsemalt saab programmi kasutada selleks, et hinnata erinevate segude termodünaamilisi ja ülekandeomadusi, arvutada keemilist tasakaalu, simuleerida põlemist, arvutada akude pingeid, modelleerida õhukeste kilede sadestamist, hinnata reaktsioonikiiruseid erinevates keskkondades, teostada kineetikasimulatsioone reaktsioonimehhanismidega, rakendada ühe-mõõtmelisi leegi mudeleid, analüüsida reaktsioonide kulgu ning modelleerida mitteideaalseid vedelikke.
Programm on üle 18 aasta vana ning selle algne arendaja on Dave Goodwin. Cantera on avatud lähtekoodiga tarkvara (open-source) ning algselt kirjutatud C++ keeles. Kaasaegsel kasutajal soovitatakse seda kasutada peamiselt Pythoni või MATLABi kaudu, kuid see on kasutatav ka C++ ja Fortran 90 keskkondades.
Cantera õppimiseks on olemas põhjalikud juhendid ja näited erinevatele tarkvaraversioonidele. Tarkvara töötab nii Windowsi, macOS-i kui ka Linuxi operatsioonisüsteemides.
Programmi struktuur
Sisendfailina kasutatakse .cti, .xml või .yaml formaati. Programmi põhiline keel on C++, mida kasutatakse skriptifailides. Rakendusprogrammide loomiseks kasutatakse seevastu enamasti MATLABit või Pythonit. Rakendusprogrammide abil saab luua erinevaid simulatsioone: kasutaja eest „peidetud“ võrrandite ja mudelite põhjal arvutab programm välja püstitatud probleemi lahenduse. Sisendfailis on kirjeldatud kõikide ainete ja segude reaktsioonid, mudelid ning eriomadused (termodünaamika, ülekandeomadused). Termodünaamiliste omaduste hulka kuuluvad temperatuur, rõhk, entalpia, siseenergia, entroopia ja keemiline potentsiaal. Gaaside ja vedelike ülekandeomadusteks on viskoossus, soojusjuhtivus, binaarsed ja mitmekomponendilised difusioonikoefitsiendid. Kineetika all mõistetakse ühtlast kineetikat; siia alla kuuluvad reaktsioonide kiirused, erinevate liikide loomise ja hävimise määrad ning tasakaalukonstandid. Programmi struktuur on esitatud joonisel 1.
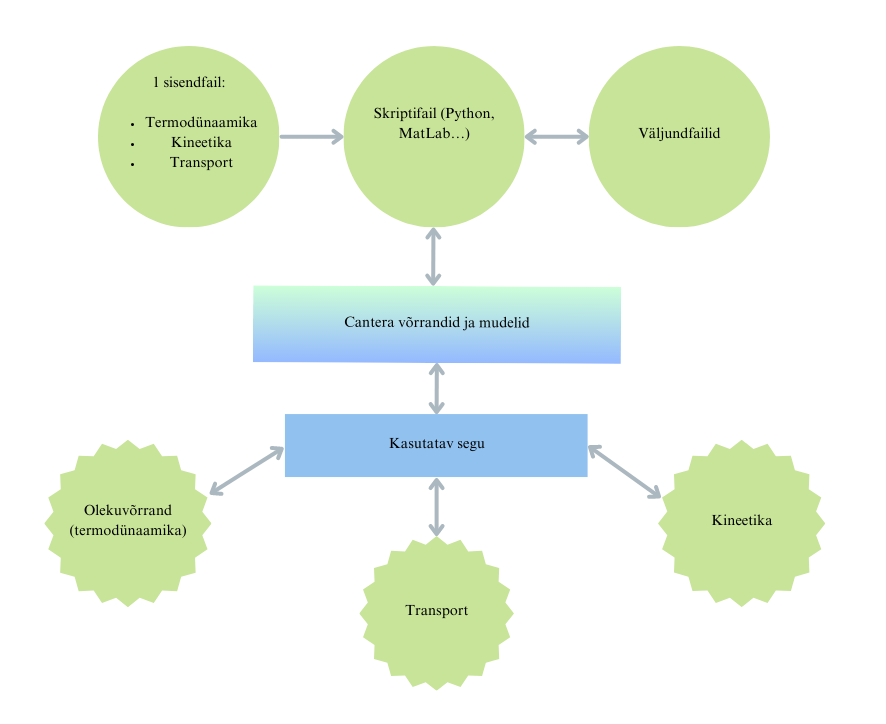
Joonis 1. Cantera struktuur.
2. Simulatsioonitarkvara teoreetilised alused – parandatud ja täpsustatud
Cantera simulatsioonitarkvara tugineb hästi teada füüsikalistele ja keemilistele põhimõtetele. Programmi abil saab modelleerida ja analüüsida mitmesuguseid protsesse, mis hõlmavad:
- termodünaamilisi arvutusi (aine olek, energia, tasakaal);
- gaaside ja vedelike ülekandeprotsesse (soojusülekanne, massiülekanne, difusioon);
- keemiliste reaktsioonide kineetikat (reaktsioonikiirused, reaktsioonimehhanismid, tasakaal).
Cantera kasutab erinevaid matemaatilisi mudeleid, mis võimaldavad simuleerida nii lihtsamaid kui ka keerukaid inseneriprotsesse. Olulisemad mudeliklassid on:
- reaktorimudelid (näiteks nullmõõtmeline, konstantse rõhuga, ideaalgaasi või pistikvoolu reaktor);
- leegimudelid (eelsegatud laminaarne leek, difusioonileek, vastuvoolu leek);
- pinnareaktsioonide mudelid (katalüütilised pinnad, keemiline sadestamine);
- mitmefaasilised süsteemid (gaas–tahkis, gaas–vedelik jne).
Kõik need mudelid kasutavad Cantera sisemisi võrrandeid ja algoritme, et lahendada termodünaamika, ülekande ja kineetika seoseid. Tulemuseks on realistlik simulatsioon, mis kirjeldab süsteemi käitumist erinevates tingimustes.
2.1. Termodünaamika
Termodünaamilised omadused sõltuvad kasutatavate ainete ning nende faaside (näiteks tahke, vedel või gaasiline faas) kohta teada olevatest lähteandmetest. Termodünaamikas kasutatakse sageli idealiseeritud mudeleid – näiteks ideaalse gaasi mudelit –, mis võimaldavad füüsikaliste süsteemide käitumist lihtsustatud kujul kirjeldada.
Termodünaamilise süsteemi oleku muutumist nimetatakse termodünaamiliseks protsessiks. Olemas on mitut tüüpi protsesse, kuid Cantera seisukohalt on eriti oluline tasakaaluline protsess, mida võib vaadelda kui seeriat järjestikustest tasakaaluolekutest, mille käigus süsteem jaotab energiat võimalikult ühtlaselt.
Selleks, et arvutada süsteemi termodünaamilisi omadusi Cantera tarkvara abil, peab kasutaja tegema järgmised sammud:
- Määrama kasutatava mudeli ning sisendid, mille põhjal omadused arvutatakse. Näiteks tuleb täpsustada, kuidas arvutatakse entalpia või entroopia temperatuurist sõltuvaid võrdlusväärtusi.
- Valima sobiva faasimudeli, mis kirjeldab, kuidas süsteemi komponendid (elemendid ja keemilised ühendid) omavahel suhestuvad. Faasimudel määrab nii süsteemi üldomaduste (temperatuur, rõhk, ruumala) kui ka lisaomaduste (siseenergia, entroopia, entalpia jmt) käitumise.
Cantera kõige levinum faasimudel on ideaalse gaasi mudel, mida kasutatakse näiteks põlemise, gaasifaasiliste protsesside või keemilise sadestamise (CVD) simuleerimisel. Mudelis on defineeritud 53 elementi ning võimalus simuleerida nende osalusel kuni 325 keemilist reaktsiooni.
2.1.1 Entalpia
Entalpia iseloomustab energiahulka, mis süsteemis on temperatuuril ja rõhul võimalik soojuseks muundada. Kuigi aine koguenenergia sõltub nii temperatuurist kui ka rõhust, ei ole kogu energia soojuseks teisendatav. Osa energiast jääb alati aine siseenergia kujul süsteemi, kuna see on seotud aine molekulaarstruktuuri ja sidemetega. Samuti ei ole kogu kineetiline energia muundatav, kuna süsteemi temperatuur läheneb ümbritseva keskkonna temperatuurile ning seeläbi väheneb võimalik soojusülekanne. Seetõttu näitab entalpia just seda osa süsteemi energiast, mida saab antud tingimustel (püsival rõhul ja temperatuuril) muuta soojusenergiaks, kuid mitte kogu süsteemi koguenenergia hulka.
Entalpia arvutamiseks kasutatakse valemit 1:
\( H = E + pV ,(1) \)
kus,
H – entalpia (J);
E – siseenergia (J);
p – rõhk (Pa);
V – maht (m3).
2.1.2. Siseenergia
Siseenergia on süsteemi kõigi osakeste kineetilise ja potentsiaalse energia summa. Seda kasutatakse kirjeldamaks energiat, mis on aine sees "peidus" ning mida ei saa otseselt väliseks tööks või soojuseks muuta ilma süsteemi olekut muutmata. Ideaalne gaas on kõige lihtsam näide siseenergia selgitamiseks. Ideaalses gaasis ei ole osakeste vahel potentsiaalset energiat, kuna osakesed ei ole omavahel seotud – nad liiguvad vabalt ja suhtlevad ainult elastsete põrgetega. Seetõttu koosneb ideaalse gaasi siseenergia üksnes osakeste kineetilisest energiast. Kineetilise molekulaarteooria järgi on gaasi temperatuur otseses seoses osakeste keskmise kineetilise energiaga. Mida kõrgem on temperatuur, seda kiiremini osakesed liiguvad ja seda suurem on siseenergia. Seetõttu sõltubki ideaalse gaasi siseenergia ainult temperatuurist (vt joonis 2).
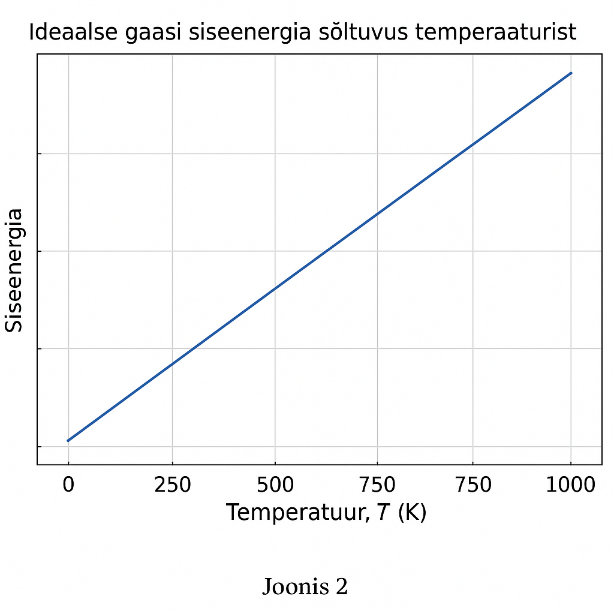
Joonis 2. Ideaalse gaasi siseenergia.
Süsteemi siseenergia avaldub valemiga 2:$$E_{\text{sys}} = \frac{3}{2} R \cdot T$$
kus,
Esys – süsteemi siseenergia (J/Kmol)
R – gaasikonstant (Kmol)
T – temperatuur (K)
2.1.3. Termodünaamika I seadus
Tänapäevane sõnastus: „Energia ei saa juurde tekkida ega ka kaduda. Energia saab muunduda ühest vormist teise või kanduda ühelt kehalt teisele.“
Kuna termodünaamika I seadus kirjeldab siseenergia muutumist ning seost soojushulga ja tehtud tööga, avaldub see järgmiselt (valem 3):
\( dU = dQ – dA , (3) \)
kus,
dU – siseenergia muut;
dQ – soojushulk;
dA – süsteemi poolt tehtud töö.
Entroopia
Entroopiat nimetatakse süsteemi juhuslikkuse või ebakorrapärasuse mõõduks. Selle mõõt sõltub süsteemi massist ning võib olla nii negatiivne, kui ka positiivne. See on seotud termodünaamika teise seadusega, mis tähendab seda, et ühe süsteemi entroopia saab väheneda ainult juhul, kui teise süsteemi entroopia vastupidi suureneb. Entroopiat arvutatakse erinevate protsesside puhul, kuid nendest kõige populaarsemad on pööratav ja isotermiline protsess.
Pööratava protsessi entroopiat arvutatakse kasutades valemit 4:
\( S=k_b (lnΩ), (4) \)
kus,
S – entroopia (J/K);
Kb – Boltzmann konstant (J/K);
Ω – süsteemi mikroolekute arv.
Isotermilise protsessi entroopia arvutamisel kasutatakse valemit 5:
\( ∆S=∆Q/T ,(5) \)
kus,
∆S – entroopia muut (J/K);
∆Q – soojuse muut (J);
T – absoluutne temp (K).
2.2. Keemiline tasakaal
Gibbsi vabaenergia on otseselt seotud keemilise tasakaaluga, kuna süsteem saavutab tasakaalu siis, kui ΔG = 0. Gibbsi vabaenergia kirjeldab energia hulka, mis on keemilises süsteemis „vaba“ ehk kasutatav kasuliku töö tegemiseks. Seetõttu iseloomustab see, kui palju energiat on reaktsioonil võimalik anda edasi tööks pärast seda, kui on arvestatud süsteemi entroopia ja entalpia mõjud.
Kui ΔG < 0, on reaktsioon iseeneselik — süsteem liigub loomulikult parema tasakaalu poole.
Kui ΔG > 0, on reaktsioon mittes-iseeneselik — selleks, et reaktsioon toimuks, on vaja välisest allikast lisajõudu või -energiat.Gibbsi vabaenergia arvutamisel kasutatakse valemit 6:
\( G = H- TS ,(6) \)
Gibbsi vabaenergia muudu arvutamisel kasutatakse valemit 7:
\( ∆G = ∆H - ∆TS , (7) \)
Iseeneseliku reaktsiooni puhul Gibbsi vabaenergia muut peab olema väiksem kui 0 ning mittes-iseeneseliku reaktsioonil Gibbsi vabaenergia muut on vastupidi suurem.
Keemilise tasakaalu (segu) arvutamisel kasutatakse valemit 8:
\( dG = \Sigma_{i=1}^{N} μ_i dn_i = 0 → \)
\( X_{k}^{equil}= \frac{P_0}{P} exp(-\frac{g_k^0(T)}{RT} + \Sigma_{l=1}^{L} n_{kl} \frac{λ_l}{RT}), (8) \)
ni – on komponendi „i“ moolide arv;
μi- on komponendi „i“ keemiline potentsiaal;
λ – soojusjuhtivus.
2.2.1. Elementaarreaktsioon
Cantera kasutab erinevaid mudeleid leekide simuleerimiseks, näiteks: Elementaarreaktsioon on üksik keemiline samm, mille käigus lähteained muunduvad produktideks vastavalt reaktsiooni stöhhiomeetriale. Sellise reaktsiooni kiiruskonstant sõltub ainult temperatuurist ning kirjeldatakse tavaliselt Arrheniuse võrrandi abil. Canteras kasutatakse selleks muudetud Arrheniuse funktsiooni, mille üldkuju on toodud valemis 9.
Reaktsiooniskeemil A + B ⇌ C + B käsitletakse protsessi kui elementaarreaktsiooni, mille kiirus ei sõltu rõhust ega keerukamatest massitegevuse efektidest; arvestatakse ainult reaktsiooni elementaarset kineetikat. Modifitseeritud Arrheniuse funktsioon on toodud valemis 9:
\( k_f = AT^b e^ \frac{-E_a}{RT}, (9) \)
kus,
kf – kiiruskonstant;
A – eksponendieelne tegur;
T – temperatuur;
b – temperatuuri eksponent;
Ea – aktivatsioonienergia;
R – gaasi konstant.
2.2.2. Mitteühtlane, gaasifaasi reaktsioon (kolmekehaline reaktsioon)
Mitteühtlane, gaasifaasis toimuv kolmekehaline reaktsioon on reaktsioonitüüp, mille üldkuju on: A + B + M ⇌ AB + M
Kolmas osake M toimib energiat neelava või loovutava „puhvrina“, mis võimaldab reaktsioonil toimuda: Stabiliseerimine: M neelab liigse energia, mis tekib A ja B ühinemisel, võimaldades moodustuda stabiilsel AB molekulil.
Lagundamine: vastupidisel suunal annab M energiat, et murda AB keemiline side ja muuta see tagasi eraldi osakesteks. Sellistes reaktsioonides mõjutavad reaktsiooni kulgu nii osakeste kontsentratsioonid kui ka keskkonna temperatuur ja rõhk. Reaktsioonikiiruse arvutamiseks kasutatakse modifitseeritud Arrheniuse võrrandit, mis on esitatud valemis 10.:
\( R_f = [A][B][M]k_f (T) ,(10) \)
Kokkupõrke efektiivsuse arvutamisel kasutatakse valemit 11, tavaliselt see vastab ühele, kuna iga konstantne kokkupõrke efektiivsus võib imenduda kiiruskoefitsiendisse kfT [13]:
\( [M] = \Sigma_{k}∈_k C_k, (11) \)
kus,
∈ - kokkupõrke efektiivsus;
Ck – on aine k kontsentratsioon.
2.2.3. Pinnareaktsioonid
Mitteühtlased reaktsioonid pindadel, arvutatakse pikendatud Arrheniuse funktsiooni abil. Reaktsioonikiiruse arvutamisel kasutatakse valemit 12:
\( k_f=AT^b exp (- \frac{E_a}{RT}) \Pi_k 10^{a_k θ_k} θ_{k}^{m_k} exp ( \frac{-E_kθ_k}{RT}), (12) \)
kus,
A, b ja Ea – muudetud Arrheniuse parameetrid;
ak, mk ja Ek – aine k katvuse sõltuvused.
2.2.4. Kleepumisreaktsioonid
Eripinna reaktsioonid, kus gaasifaasi molekulide ja pindade omavaheliste kokkupõrgete tulemusena kleepub gaasifaasi molekul pinnale. Kleepumiskoefitsienti arvutamisel kasutatakse valemit 13:
\( γ = aT^b e^{-c/RT}, (13) \)
kus,
γ – kleepumiskoefitsient;
a, b, c – kindla reaktsiooni konstandid (nende väärtused peavad olema täpsustatud, et kleepumiskoefitsient oleks kõikide temperatuuride jaoks vahemikus 0 - 1).
Kleepumiskoefitsient sõltub reaktsioonikiirusest (valem 14):
\( k_f = \frac{γ}{ Г_ {tot}^{m}}√ \frac{RT}{2πW}, (14) \)
kus,
\( Г_ {tot}^{m} \) – kogu molaarne tihedus;
m - kõigi pinnareagendi stöhhiomeetriliste koefitsientide summa;
W – gaasifaasi molekulmass.
2.3. Ülekandeprotsessid (transport properties)
Sarnaselt termodünaamika kategooriaga sõltuvad gaaside ja vedelike ülekandeomaduste ning ülekandeprotsesside (näiteks soojusülekanne, massiülekanne, impulsiülekanne) arvutamisel saadud tulemused kasutatavate ainete ja faaside lähteandmetest. Programmi kasutaja peab:
Määrama ülekandemudeli ning sisestama vajalikud lähteandmed selle kohta, kuidas konkreetse liigi ülekandeomadusi arvutatakse. Näiteks võib kasutaja sisestada parameetrid, mille alusel Cantera arvutab kokkupõrkeintegraale Lennard–Jonesi potentsiaali põhjal.
Valima sobiva faasimudeli, et kirjeldada, kuidas erinevad ained omavahel käituvad ning kuidas määrata antud termodünaamilises olekus faasikeskmistatud omadusi (nt viskoossus, soojusjuhtivus) ja eriomadusi (nt difusioonikoefitsiendid).
Cantera kasutab kahte ülekandemudelit — multi ja segu (mix). Nende erinevused seisnevad gaasiomaduste ja difusioonikoefitsientide arvutamise meetodites.
2.3.1. Ülekandemudel: multi
- Ei kasuta ligikaudseid lihtsustusi.
- Hõlmab ka Soreti efekti (temperatuurigradientidest põhjustatud difusioon).
- Iga mitmekomponendilise difusioonikoefitsiendi väärtus leitakse maatriksi inversiooni kaudu.
- Erinevate liikide difusioonikiirused mõjutavad üksteist, seega on see mudel täpsem ja arvutuslikult keerukam.
2.3.2. Ülekandemudel: segu (mix)
- Kasutab lihtsustatud seadusi ja võrrandeid.
- Eeldab, et liikide difusioonikiirused on üksteisest sõltumatud.
- Arvutuslikult vähem nõudlik, kuid füüsikaliselt vähem täpne kui multi-mudel. Soret effect
2.4. Difusiooni koefitsient
Difusioon on protsess, mille käigus osakesed liiguvad kõrgema kontsentratsiooniga piirkonnast madalama kontsentratsiooniga piirkonda, kuni kontsentratsioon ühtlustub. See toimub osakeste juhusliku termilise liikumise tulemusena ning on aineülekande üks olulisemaid põhiprotsesse gaasides, vedelikes ja isegi tahketes materjalides.
Difusioonikoefitsient on füüsikaline konstant, mis iseloomustab, kui kiiresti osakesed teatud keskkonnas difundeeruvad. Selle väärtus sõltub mitmest tegurist, sh: molekuli suurus, molekulidevahelised vastasmõjud, hajutava keskkonna omadused, temperatuur ja rõhk.
Eristatakse kahte liiki difusiooni:
Enesedifusioon – üksikute molekulide liikumine läbi sama aine molekulikihi (nt O₂ molekulid difundeeruvad läbi O₂ gaasi).
Interdifusioon – erinevate ainete või komponentide vastastikune difusioon segus (nt O₂ ja N₂ liikumine õhus).
Alljärgnevad tabelid toovad näiteid difusioonikoefitsientidest erinevates gaasisüsteemides (vt tabel 1 ja tabel 2).
Tabel 1. Enesedifusioon Da. Keskkonnatemperatuur 237 K, rõhk 0.1 MPa
|
Gaas |
DA, cm2/s |
Gaas |
DA, cm2/s |
Gaas |
DA, cm2/s |
|
H2 |
1.604 |
O2 |
0.192 |
H2O |
0.276 |
|
He |
1.386 |
N2 |
0.155 |
CH4 |
0.188 |
|
Ar |
0.157 |
CO2 |
0.106 |
NH3 |
0.192 |
Tabel 2. Interdifusiooni koefitsient
|
Gaas (A) |
Gaas (B) |
P, mmH2O |
T, K |
DAB, cm2/s |
|
H2 |
He |
760 |
298 |
1.64 |
|
Ar |
He |
751 |
288 |
0.703 |
|
N2 |
CO2 |
760 |
288 |
0.158 |
|
H2O |
õhk |
760 |
273 |
0.219 |
|
H2 |
N2 |
760 |
288 |
0.743 |
|
H2O |
CO2 |
760 |
273 |
0.146 |
2.5. Reaktorid
Cantera abil saab modelleerida nullmõõtmelisi reaktoreid ning nende vastastikmõju ümbritseva keskkonnaga. Programmi sisseehitatud võrrandid võimaldavad simuleerida mitut tüüpi reaktoreid, sealhulgas:
- muutumatu mahu reaktor (constant volume reactor)
- muutumatu rõhu reaktor (constant pressure reactor)
- ideaalse gaasi reaktor
- ideaalse gaasi reaktor (muutmatul rõhul),
- väljatõrjereaktor (plug flow reactor, PFR),
- laiendatav reaktor (extensible reactor),
- kohandatud reaktor (custom reactor).
Reaktorite ja ümbritseva keskkonna vahel saab kirjeldada järgmiseid vastastikmõjusid:
- Paisumis- ja komprimeerimistööd – reaktori seinte liigutamine muudab süsteemi mahtuvust. Töö võib toimuda nii reaktori sees kui ka selle piirpindadel.
- Soojusülekanne – läbi reaktori seinte võib määrata soovitud soojusvoo või soojusülekandeteguri.
- Massiülekanne – reaktoril võib olla üks või mitu sisend- ja väljalaskeava, mille kaudu aine sisse voolab või väljub.
- Pinnamõjud – reaktori seinad võivad olla keemiliselt aktiivsed ja mõjutada reaktsioonide kulgemist (näiteks katalüütilised pinnareaktsioonid).
2.5.1. Reaktorite seinad (walls)
Reaktorisein (wall) eraldab:
- kas kahte reaktorit
- või reaktori ja veesärgi
Veehoidla (reservoir) on fikseeritud olekuga süsteem, mis määrab reaktorisse siseneva massvoolu temperatuuri, rõhu ja koostise. Samuti eeldatakse, et reaktorist väljuvad vood jõuavad lõpuks tagasi veehoidlasse.
Reaktorisein võib juhtida soojust kahe süsteemi vahel või liikuda näiteks kolvina, muutes reaktori mahtu, omada piiratud pinda, mis mõjutab soojuse ja töö ülekannet. Seina kiiruse arvutamisel kasutatakse valemit 15:
\( v=K(P_{vasak}-P_{parem})+v_0(t), (15) \)
kus,
v – kiirus (positiivne, kui sein liigub paremale);
K – seina laienemiskiiruse parameeter, mittenegatiivne konstant;
v0(t) – kiiruse funktsioon. Seina soojusvoo arvutamisel kasutatakse valemit 16 [19]:
Seina soojusvoo arvutamisel kasutatakse valemit 16 [19]:
\( q=U(T_{vasak}-T_{parem} )+ϵσ(T_{vasak}^{4} - T_{parem}^{4})+q_0 (t), (16) \)
kus,
U – üldine soojusülekandetegur (positiivne, kui soojus liigub vasakpoolsest reaktorist parempoolsesse reaktorisse);
ϵ – emissioon;
q0 (t) - soojusvoo funktsioon.
2.5.2. Mahu reaktor
Mahureaktor on ühtlane (homogeenne) nullmõõtmeline reaktor, mis käitub füüsikas tuntud kinnise süsteemina – see tähendab, et reaktoril puuduvad sisse- ja väljalaskeavad ning süsteemi kogumass ei muutu. Reaktori maht on fikseeritud ning seinad on vaikimisi adiabaatilised (ei toimu soojusülekannet) ja keemiliselt inaktiivsed (ei toimu pinnareaktsioone). See lihtsustab märkimisväärselt modelleerimist: kogu reaktoriruumi kirjeldavad ühed ja samad termodünaamilised, kineetilised ja keemilise tasakaalu võrrandid.
Cantera võimaldab aga seda baasreaktorit hõlpsasti kohandada. Lisades vajalikke elemente – näiteks seinad, massivoolu regulaatori, vooluseadme/klapi või soojusülekande komponendid – saab muuta süsteemi järgmistes aspektides:
lisada või eemaldada massi (muutes süsteemi avatud süsteemiks)
võimaldada soojusülekannet läbi seinte
arvestada seinareaktsioone
muuta mahtu läbi liikuvate seinade.
Seega on reguleerimismahu reaktor Cantera kõige aluselisem reaktoritüüp, millele saab vajadusel lisada dünaamilisi protsesse, kuid mille algne konfiguratsioon vastab klassikalisele termodünaamika suletud, adiabaatilisele süsteemile.Antud reaktorit määravad neli kindlat parameetri:
- m (mass, kg);
- V (mahtuvus, m3);
- U (siseenergia, J);
- Yk (iga liigi massifraktsioonid). [20]:
Kogumass muutub reaktori sisse- ja väljalaskeavade voolamise ja ühtlaste faasiliikide tootmise pärast, matemaatiline näidis, valem 17 [20]:
\( \frac{dm}{dt}= \Sigma_{in} m ̇_{in}-\Sigma_{out}m ̇_{out}+m ̇_{wall}, (17) \)
kus,
In/out – on kõikide sisendite ja väljalaskeavade summa.
Mahtuvus muutub seinade liikumise pärast, matemaatiline näidis, valem 18 [20]:
\( \frac{dV}{dt}=∑_wf_wA_wv_w (t), (18) \)
kus,
fw – näitab seina otspinda (±1, sõltub sellest, kas seina liikumisel reaktori maht suureneb või väheneb);
Aw – seina pindala;
vw(t) – seina kiirus, kindla aja funktsioonina.
Kogu siseenergia võrrand, valem 19 [20]:
\( \frac{dU}{dt}=-p\frac{dV}{dt}+Q ̇+∑_{in}+m ̇_{in}h_{in}-h∑_{out}m ̇_{out}, (19) \)
kus,
Q – süsteemi soojuse netomäär.
2.6. Leegid
Cantera kasutab erinevaid mudeleid leekide simuleerimiseks, näiteks:
- eelsegatud ja vabalt levivad laminaarsed leegid;
- eelsegatud leegid, mis on põletiga stabiliseeritud;
- vastuvoolu difusioonileegid;
- eelsegatud-sunnitud vastuvoolu leegid.
Samuti Cantera võimaldab simuleerida pinnareaktsioone, et näidata selliseid protsesse nagu keemiline sadestamine või põlemine katalüütilisel pinnal.
Seisaku reguleerimine
Programm modelleerib leeke, mis on stabiliseeritud teljesümmeetrilises seiskumisvoolus. Sellises voolus väheneb voolukiirus seiskumispunkti lähenedes nullini. Cantera kasutab seda geomeetriat, et lihtsustada arvutust: kolmemõõtmelised juhtvõrrandid taandatakse ühe mõõtmega lahendatavaks süsteemiks. See võimaldab koostada täpseid, kuid arvutuslikult efektiivseid mudeleid. Seisaku reguleerimisel kasutatakse valemeid 20, 21, 22 ja 23:
1. Jätkuvus, valem 20;
2. Radiaalne impulss, valem 21;
3. Energia, valem 22;
4. Liigid, valem 23.
\( \frac{∂ρu}{∂z}+2ρV =0, (20) \\ ρu\frac{∂V}{∂z}+ρV^2=-Λ+ \frac{∂}{∂z}(μ \frac{∂V}{∂z}), (21) \\ ρc_p u \frac{∂T}{∂z}=\frac{∂}{∂z}(λ \frac{∂T}{∂z})-∑_kj_k c_{p,k}\frac{∂T}{∂z}-∑_k h_k W_k w ̇_k, (22)\\ ρu \frac{∂Y_k}{∂z}=-\frac{∂j_k}{∂z}+W_k w ̇_k , (23) \)
kus,
ρ – tihedus;
u – aksiaalne kiirus;
v – radiaalne kiirus;
V = v/r – skaleeritud radiaalkiirus;
Λ – rõhu omaväärtus (sõltumatu z arvust);
μ – dünaamiline viskoossus;
cp – soojusmahtuvus konstantsel rõhul;
T – temperatuur;
λ – soojusjuhtivus;
Yk - massifraktsioon (k);
Jk - difuusne massivoog (k);
Cp,k –erisoojusmahtuvus (k)
hk – entalpia (k);
Wk – molekulmass (k);
w - molaarne tootmismäär, tuletis (k).